Background
In computer coding, it’s super important to write really good code. Good code doesn’t just make programs run faster, it also helps developers work better. But figuring out what makes code good can be tricky, and it’s not just about making things run quickly.
Good code has things like being easy to test, easy to keep up, easy to use again, and easy to add more stuff to. These things are like measuring sticks for how tough and reliable the code is. But knowing how to make code like that isn’t always clear, so we look into ways to help us write clean code.
One cool way to do this is by using functional programming. It’s a style of coding inspired by math, and it’s all about using expressions and putting functions together. We separate pure functions, which only do one thing and don’t mess with anything else, from impure ones, which do more things. This helps make our code not just easy to understand but also makes testing and modifying way simpler.
In ABAP (a programming language), Object-Oriented ABAP is a great way to use functional programming ideas. It’s not a perfect solution for everything, but it really helps us think about problems in new ways.
Functional Programming in A Nutshell
Functional programming is programming using functions.
Functional programming is like building with LEGO blocks, combining functions to build a new and different use of function.
Let’s take a look at the provided Haskell code examples, showcasing the essence of functional programming:
even :: (Integral a) => a -> Bool
even x
| x `mod` 2 == 0 = True
| otherwise = False
Here, I’ve defined a function called even that takes an integral value, x, and returns a boolean indicating whether x is even. I’ve used guards (|) to make the code concise and expressive which is the main characteristic of functional programming.
odd :: (Integral a) => a -> Bool
odd = not . even
In this example, I leverage the composition operator (.) to define the odd function succinctly. I take advantage of the previously defined even function, showcasing the power of composing functions to create new ones.
filter :: (a -> Bool) -> [a] -> [a]
filter _ [] = []
filter pred (x:xs)
| pred x = x : filter pred xs
| otherwise = filter pred xs
The filter function showcases a common higher-order function in functional programming. I take a predicate function,, and a list of any type [a], returning a new list containing only the elements that satisfy the predicate. This serves as a clear example of functional programming’s emphasis on using higher-order functions for concise and expressive code.
In this function, I highlight the recursive technique — a fundamental aspect of functional programming. Recursion is not only a technical approach but also a distinctive way of thinking. Embracing recursion allows me to break down complex problems into simpler, more manageable sub-problems, fostering code elegance and a deeper understanding of functional programming principles.
ghci> filter odd [1..100]
[1,3,5,7,9,11,13,15,17,19,21,23,25,27,29,31,33,35,37,39,41,43,45,47,49,51,53,55,57,59,61,63,65,67,69,71,73,75,77,79,81,83,85,87,89,91,93,95,97,99]
ghci> filter even [1..100]
[2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32,34,36,38,40,42,44,46,48,50,52,54,56,58,60,62,64,66,68,70,72,74,76,78,80,82,84,86,88,90,92,94,96,98,100]
These examples demonstrate Haskell’s functional programming features, emphasizing the concise and declarative nature of the code. The use of higher-order functions, immutability, and function composition contributes to the readability and maintainability of the codebase. These principles form the basis for our exploration of functional programming in Object-Oriented ABAP in the subsequent sections.
Translating Functional Programming Concepts: Haskell to ABAP
Let’s seamlessly translate the Haskell code above into ABAP, aiming for a natural adaptation that captures the essence of functional programming concepts applied in an Object-Oriented (OO) paradigm, specifically within the ABAP language.
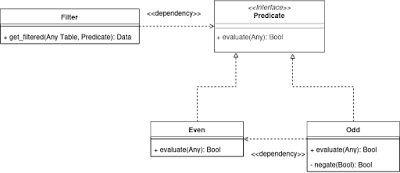
Here is the code implementation,
ABAP
INTERFACE zif_predicate
PUBLIC .
METHODS evaluate IMPORTING value TYPE any
RETURNING VALUE(result) TYPE abap_bool.
ENDINTERFACE.
The zif_predicate interface serves as a contract or blueprint for classes that implement a specific method signature, in this case, the evaluate method. I’ve defined it to establish a common contract that the zcl_predicate_even and zcl_predicate_odd classes adhere to.
The purpose of this interface is to declare a method, evaluate, that takes a value and returns a boolean result. Its usage lies in ensuring that all classes implementing this interface adhere to a consistent contract. In this context, I use the interface to implement a higher-order function through the application of dependency injection.
Even Predicate in Haskell vs ABAP
Haskell
even :: (Integral a) => a -> Bool
even x
| x `mod` 2 == 0 = True
| otherwise = False
ABAP
CLASS zcl_predicate_even DEFINITION
PUBLIC
FINAL
CREATE PUBLIC .
PUBLIC SECTION.
INTERFACES zif_predicate.
PROTECTED SECTION.
PRIVATE SECTION.
ENDCLASS.
CLASS zcl_predicate_even IMPLEMENTATION.
METHOD zif_predicate~evaluate.
FIELD-SYMBOLS <value> TYPE i.
ASSIGN value TO <value>.
result = COND #( WHEN <value> MOD 2 = 0
THEN abap_true
ELSE abap_false ).
ENDMETHOD.
ENDCLASS.
In both languages, I’ve defined a predicate to check if a number is even. The ABAP implementation uses an interface zif_predicate to establish a common contract and the evaluate method mirrors the Haskell logic. Additionally, I exemplify the application of dynamic programming in ABAP to adeptly handle generic data types, which is common in the functional programming world.
Odd Predicate in Haskell vs ABAP
Haskell
odd :: (Integral a) => a -> Bool
odd = not . even
ABAP
CLASS zcl_predicate_odd DEFINITION
PUBLIC
FINAL
CREATE PUBLIC .
PUBLIC SECTION.
INTERFACES zif_predicate.
PROTECTED SECTION.
PRIVATE SECTION.
METHODS negate IMPORTING truth TYPE abap_bool
RETURNING VALUE(result) TYPE abap_bool.
ENDCLASS.
CLASS zcl_predicate_odd IMPLEMENTATION.
METHOD zif_predicate~evaluate.
result = negate(
CAST zif_predicate(
NEW zcl_predicate_even( )
)->evaluate( value = value ) ).
ENDMETHOD.
METHOD negate.
result = COND #( WHEN truth = abap_true
THEN abap_false
ELSE abap_true ).
ENDMETHOD.
ENDCLASS.
Here, I define the odd predicate in Haskell by negating the even predicate. In ABAP, I encapsulate this logic in the zcl_predicate_odd class, which internally leverages the zcl_predicate_even class to evaluate evenness and then negate it. In this part, I use function composition in both languages. In functional programming, I believe function composition is the key to handling complexity.
Filtering Elements in a List in Haskell vs ABAP
Haskell
filter :: (a -> Bool) -> [a] -> [a]
filter _ [] = []
filter pred (x:xs)
| pred x = x : filter pred xs
| otherwise = filter pred xs
ABAP
CLASS zcl_filter DEFINITION
PUBLIC
FINAL
CREATE PUBLIC .
PUBLIC SECTION.
METHODS get_filtered IMPORTING predicate TYPE REF TO zif_predicate
value_tab TYPE ANY TABLE
RETURNING VALUE(result) TYPE REF TO data.
PROTECTED SECTION.
PRIVATE SECTION.
ENDCLASS.
CLASS zcl_filter IMPLEMENTATION.
METHOD get_filtered.
FIELD-SYMBOLS <result_tab> LIKE value_tab.
CREATE DATA result LIKE value_tab.
ASSIGN result->* TO <result_tab>.
LOOP AT value_tab ASSIGNING FIELD-SYMBOL(<value>).
IF predicate->evaluate( <value> ) = abap_false.
CONTINUE.
ELSE.
INSERT <value> INTO TABLE <result_tab>.
ENDIF.
ENDLOOP.
ENDMETHOD.
ENDCLASS.
In both languages, I’ve implemented the filter function as a higher-order function. In Haskell, it operates on lists, and in ABAP, it uses a generic table structure. The ABAP implementation defines a class zcl_filter that takes a predicate and a table of values, returning a filtered result.
In imperative programming languages, including ABAP, I always prefer to use loops over recursive methods. Handling generic data here becomes more complex but still acceptable. In this method, I observe the utilization of higher-order functions in ABAP through the implementation of dependency injection.
While in functional programming, functions are considered first-class citizens, in Object-Oriented Programming (OOP), objects take on this primary role.
Usage in GHCi vs ABAP Demo
ABAP
CLASS zcl_demo_fp DEFINITION
PUBLIC
FINAL
CREATE PUBLIC .
PUBLIC SECTION.
INTERFACES if_oo_adt_classrun.
PROTECTED SECTION.
PRIVATE SECTION.
ENDCLASS.
CLASS zcl_demo_fp IMPLEMENTATION.
METHOD if_oo_adt_classrun~main.
TYPES ty_t_integer TYPE STANDARD TABLE OF i WITH EMPTY KEY.
DATA(filter) = NEW zcl_filter( ).
DATA(even) = CAST zif_predicate( NEW zcl_predicate_even( ) ).
DATA(odd) = CAST zif_predicate( NEW zcl_predicate_odd( ) ).
DATA value_tab TYPE ty_t_integer.
" get even number from 1 to 100
out->write( `Even Numbers` ).
DATA(even_number) = filter->get_filtered(
predicate = even
value_tab = VALUE ty_t_integer( FOR i = 1 THEN i + 1 UNTIL i = 100
( i ) )
).
ASSIGN even_number->* TO FIELD-SYMBOL(<even_number>).
IF <even_number> IS ASSIGNED.
value_tab = CORRESPONDING #( <even_number> ).
DATA(string_even) = REDUCE string( INIT evens TYPE string
FOR <even> IN value_tab
NEXT
evens = COND #( WHEN evens IS INITIAL
THEN <even>
ELSE |{ evens }, { <even> }| ) ).
out->write(
EXPORTING
data = |[{ string_even }]| ).
ENDIF.
" get odd number from 1 to 100
out->write( `Odd Numbers` ).
DATA(odd_number) = filter->get_filtered(
predicate = odd
value_tab = VALUE ty_t_integer( FOR i = 1 THEN i + 1 UNTIL i = 100
( i ) )
).
ASSIGN odd_number->* TO FIELD-SYMBOL(<odd_number>).
IF <odd_number> IS ASSIGNED.
CLEAR value_tab.
value_tab = CORRESPONDING #( <odd_number> ).
DATA(string_odd) = REDUCE string( INIT odds TYPE string
FOR <odd> IN value_tab
NEXT
odds = COND #( WHEN odds IS INITIAL
THEN <odd>
ELSE |{ odds }, { <odd> }| ) ).
out->write(
EXPORTING
data = |[{ string_odd }]| ).
ENDIF.
ENDMETHOD.
ENDCLASS.
The final part of my ABAP code (zcl_demo_fp) showcases the usage of the defined classes and predicates, similar to how the examples were demonstrated in GHCi for Haskell. In my demo class, I create instances of the filter, even, and odd predicates, apply them to a range of integers, and output the results.
Conclusion
In this chapter, we explored basic ideas in functional programming, focusing on two important things: higher-order functions and function composition. Here’s what you need to remember:
Functional Programming Insights: We learned why higher-order functions and function composition are super important in functional programming. Understanding these concepts helps us make the most out of functional programming.
Natural Implementation in Object-Oriented Programming: Some people think that functional programming is only for certain languages, but I showed how these ideas can work smoothly in Object-Oriented Programming (OOP). Using dependency injection, I made higher-order functions work well. With functional method composition, I found a natural way to combine functions (using functional method) in an OOP setup.
Looking Ahead:
We’ve made good progress with using functional programming ideas, but there’s more to learn. To write really great code, we need to understand things in a more detailed way. So, in the next part, we’re going to look at a real-world example. We’ll explore how to design things in a smart way, using ideas from functional programming. Our goal is to show how these ideas can help us create clean code.
Our adventure is not finished yet. We’re ready to go deeper into the mix of functional programming and Object-Oriented ABAP. This could change the way we usually design and make software. Stick around as we uncover more about how these ideas can make a big difference in how we create software that works well.

No comments:
Post a Comment